Il concetto di momento angolare, così come quello di impulso, fa parte ormai dei concetti innati che ci appartengono.

Per chiarirlo meglio, prendiamo un tuffatore che si lancia da un trampolino molto alto. Durante il tuffo comincia a ruotare, non appena si abbraccia le gambe la sua velocità di rotazione aumenta, per poi ridursi nuovamente quando, prima di incontrare l’acqua, si distende.
La stessa cosa accade ad una pattinatrice che, cominciando le piroette a braccia larghe, le ritira lungo il corpo per aumentare la propria velocità di rotazione.
Questi due esempi ci permettono di introdurre il concetto di momento angolare, legato alla rotazione di un corpo intorno ad un asse e per il quale vale una legge di conservazione analoga a quella dell’energia e della quantità di moto.

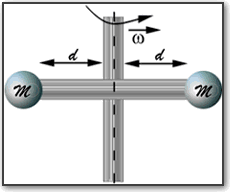
Vediamo di capire meglio che cosa sia il momento angolare con un esempio più semplice del tuffatore, anche se meno noto: il manubrio. Questo oggetto è composto da due sbarre poco pesanti unite insieme a forma di croce; lungo i due bracci di una sbarra ci sono due palle molto pesanti poste simmetricamente rispetto all’altra sbarra. Il manubrio può ruotare liberamente intorno alla sbarra su cui non abbiamo fissato le sfere (asse di rotazione).

Diamo ora una spinta al manubrio per farlo cominciare a girare, così le nostre sfere cominceranno a ruotare con velocità di rotazione (o angolare) .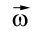
Se durante la rotazione attacchiamo altre due palle, una per lato (ad esempio con una calamita per non esercitare forze sul sistema), notiamo che il valore di 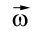si dimezza. Se invece aumentiamo la distanza delle palle dall’asse, ad esempio, del doppio, allora la velocità angolare si riduce ad 1/4 del suo valore.

Abbiamo così imparato che conservando il momento angolare, cioè non applicando forze esterne sul nostro manubrio, raddoppiando la massa (il numero di palline perchè le sbarre sono molto leggere) si dimezza 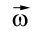, mentre raddoppiando la distanza delle palline dall’asse, 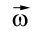si riduce ad 1/4 del suo valore iniziale. Eseguendo una serie di misure cambiando le masse e le distanze dall’asse si scopre che la quantità che non cambia mai è: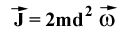 (2 perché ho due masse m uguali, d è la distanza dall’asse).
Nel caso del tuffatore e della pattinatrice le cose non sono così semplici perchè la massa è distribuita lungo tutto il corpo, e non agli estremi come nell’esempio, ma tralasciamo queste complicazioni.
Come per l'impulso, si ha la conservazione del momento angolare in tutti i processi in cui non intervengono forze esterne sul sistema (a meno che non siano applicate sull’asse).

Notiamo che 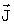è un vettore in quanto la velocità angolare è riferita ad un asse orientato nello spazio lungo una direzione non definita a priori.